浅谈KMP算法

Resory

发布于：2020年12月26日

$\text{KMP}$ 算法是一种单模式串匹配算法，由 $\mathsf{D.E.Knuth}$、$\mathsf{J.H.Morris}$ 和 $\mathsf{V.R.Pratt}$ 在 1977 年共同提出，可以在 $\Theta(n+m)$ 的时间复杂度内实现单个模式串的匹配。

模式串匹配

所谓模式串匹配，就是给定一个主串 S 以及一个模式串 P ，查询 P 在 S 中出现的次数以及位置。例如：

$\begin{aligned} S: \qquad & \texttt{ABABCBAABA} \\ P: \qquad & \texttt{ABA} \end{aligned}$

主串为 ABABCBAABA，模式串为ABA，匹配结果是出现两次，分别从下标0和8开始，其中主串下标从0开始。

我们先从最朴素的暴力算法（BF算法）说起。

暴力（Brute-Force算法）

最朴素的算法就是，对于每个位置循环匹配，遇到不相同的字符就返回。

int bf(string s,string p) {
    int cnt = 0,n = s.size(),m = p.size();
    for(int i = 0;i < n - m + 1;i ++) {
        for(int j = 0;j < m;j ++)
            if(s[i + j] != p[j]) break;
        if(j == m) ++ cnt,printf("pos=%d\n",i);
    }
    return cnt;
}

还是刚才那个例子，暴力算法的运行流程如下：

$\begin{aligned} S: \qquad & \texttt{ABABCBAABA} \\ P: \qquad & \texttt{ABA} \end{aligned}$

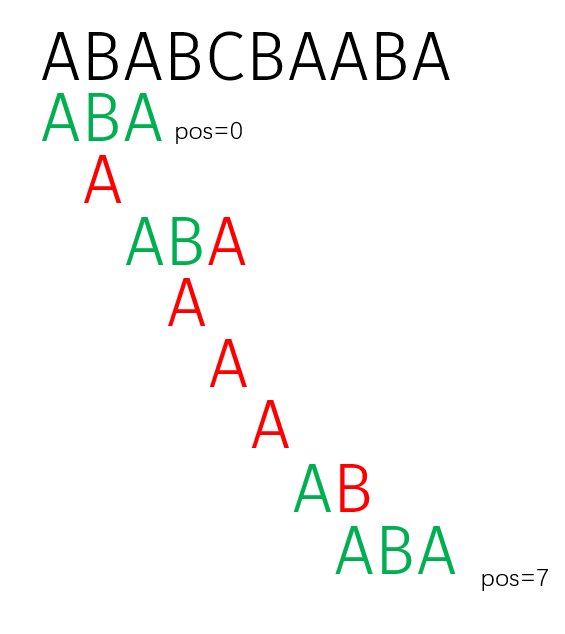
这种方法的时间复杂度最坏为 $O(nm)$，最好为 $O(n)$，并且很容易被卡，不能接受。

暴力算法的优化思路

注意到，暴力匹配每次失配时都会将开始的下标增加1，而配对多次时这样的弊端就十分明显了。因此，我们要考虑降低比较的趟数。我们发现，如果匹配 $S[l\dots (l+\operatorname{len}(P)-1)]$ 是在下标 $r$ 处失败的，那么主串的子串 $S[l\dots r - 1]$ 一定等于 $P[0\dots r-l]$！比如：

$\begin{aligned} S: \qquad & \texttt{ALGORITHM} \\ P: \qquad & \texttt{ALPHA} \end{aligned}$

$\small\text{（绿色这一段是相等的）}$

于是这能告诉我们，主串的某个子串等于格式串的某个前缀。我们就要用这个信息跳过一些不可能成功的比较。

前缀函数

对于一个字符串 $s$，它的前缀函数 $\pi$ 定义为一个长度为 $\operatorname{len}(s)$ 的数组（在 OI 中一般写作nxt数组），其中 $\pi(i)$ 的定义为 $s$ 的子串 $s[0\dots i]$ 中最长的相等的真前缀和真后缀的长度。用数学语言描述如下：

$\pi(i)=\max_{k=0\dots i} \left\{k:s[0\dots (k-1)]=s[(i-k+1)\dots i]\right\}$

举个例子：若 $s$ 等于abababc，则：

$\pi(0)=0$，因为子串a没有相等的真前缀和真后缀；
$\pi(1)=0$，因为子串ab没有相等的真前缀和真后缀；
$\pi(2)=1$，因为子串aba最长的相等的真前缀和真后缀a长度为 $1$；
$\pi(3)=2$，因为子串abab最长的相等的真前缀和真后缀ab长度为 $2$；
$\pi(4)=3$，因为子串ababa最长的相等的真前缀和真后缀aba长度为 $3$；
$\pi(5)=4$，因为子串ababab最长的相等的真前缀和真后缀abab长度为 $4$；
$\pi(6)=0$，因为子串abababc没有相等的真前缀和真后缀。

综上，abababc的前缀函数值为 $[0,0,1,2,3,0]$。

计算前缀函数

直接按照函数定义计算：

循环变量 $i\Rightarrow 1 \operatorname{to} n$ 计算 $\pi(i)$ 的值（此时 $\pi(0)$ 被默认赋值为 $0$）；
令内层循环变量 $j \Rightarrow i \operatorname{to}0$，表示 $\pi(i)$ 的值。如果当前长度下真前缀和真后缀相等（即 $s[0\dots(j-1)]=s[(i-j+1)\dots i]$），那么停止循环， $\pi(i)=j$。

查看代码

void getNxt(string s,int nxt[]) {
    int n = s.size();
    for(int i = 1;i < n;i ++) {
        for(int j = i;j >= 0;j --)
            if(s.substr(0,j) == s.substr(i - j + 1,j)) break;
        nxt[i] = j;
    }
    return ;
}

由于substr函数的时间复杂度为 $O(n)$，显然这种算法的时间复杂度为 $O(n^3)$，不能接受，考虑优化。

考虑从 $\pi(i-1)$ 与 $\pi(i)$ 的关系入手。分 $s[\pi(i-1)]=s[i]$ 和 $s[\pi(i-1)]\not=s[i]$ 两种情况讨论。

$s[\pi(i-1)]=s[i]$，即：
$\underbrace{\overbrace{s_0\ s_1\ s_2}^{\pi(i-1)=3}\ s_3}_{\pi(i)=4}\ \dots\ \underbrace{\overbrace{ s_{i-3}\ s_{i-2}\ s_{i-1}}^{\pi(i-1)=3}\ s_{i}}_{\pi(i)=4}\quad \left(s_3=s_i\right)$
显然可以得出：$\pi(i)=\pi(i-1)+1$。
$s[\pi(i-1)]\not=s[i]$，即：
$\overbrace{\underbrace{s_0\ s_1}_{j=2}\ s_2}^{\pi(i-1)=3}\ s_3\ \dots\ \overbrace{s_{i-3}\ \underbrace{s_{i-2}\ s_{i-1}}_{j=2}}^{\pi(i-1)=3}\ s_i\quad \left(s_3\not=s_i\right)$
则我们继续找出 $s[0\dots(i-1)]$ 中第二长的相等的真前缀和真后缀，记这个长度为 $j$。再次比较 $s[i]$ 和 $s[j]$。如果相等，则 $\pi(i)=j+1$。否则，继续找出 $s[0\dots(i-1)]$ 中第二长的相等的真前缀和真后缀，长度为 $j_2$，继续比较 $s[i]$ 和 $s[j_2]$。如此循环往复，直至 $j_k=0$ 或 $s[i]=s[j_k]$ 为止，此时 $\pi(i)=j_k+[s[i]=s[j_k]]$ （中括号表示当括号内表达式为真时值为 $1$，否则值为 $0$）。

观察上图我们可以发现：$s[0\dots(j-1)]=s[(i-j)\dots(i-1)]$。又根据前缀函数的性质，我们可以得出：$s[(i-j)\dots(j-1)]=s[(\pi(i-1)-j)\dots(\pi(i-1)-1)]$。等量代换后可以得到：$s[0\dots(j-1)]=s[(\pi(i-1)-j)\dots(\pi(i-1)-1)]$。我们发现，$j$ 的值恰好符合 $\pi(\pi(i-1)-1)$ 的定义！同理也可以得出 $j_2=\pi(j-1)$。由此我们可以得出，$j_k=\pi(j_{k-1}-1)$。所以我们可以循环迭代这个过程，求出前缀函数的值。

查看代码

void getNxt(string s,int nxt[]) {
    int n = s.size();
    for(int i = 1,j = 0;i < n;i ++) {
        while(j > 0 && s[i] != s[j]) j = nxt[j - 1];
        if(s[i] == s[j]) j ++;
        nxt[i] = j;
    }
    return ;
}

不难得出，求解前缀函数的时间复杂度为 $\Theta(m)$。

KMP算法

$\text{KMP}$ 算法的精髓在于，通过已经匹配完成的字符段，利用前缀函数的性质，跳过不可能的匹配，从而节省时间。

直接看个例子：

$\begin{aligned} S: \qquad & \texttt{BABCBABCABCAABCABCABCACABC} \\ P: \qquad & \texttt{ABCABCACAB} \end{aligned} \\ \quad$

我们首先对模式串 P 求解前缀函数，得到 $\{0,0,0,1,2,3,4,0,1,2\}$。接着，按照 $i\Rightarrow 0 \operatorname{to} n, j\Rightarrow 0 \operatorname{to} m$ 依次匹配 $S[i]$ 和 $P[i+j]$。当 $i=0$ 时：

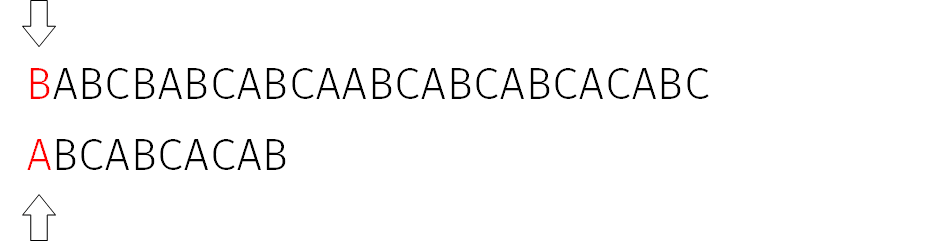
此时，$S[0]\not=P[0]$，在 $j=0$ 处失配。于是我们将 $i$ 指针右移一格，继续匹配：

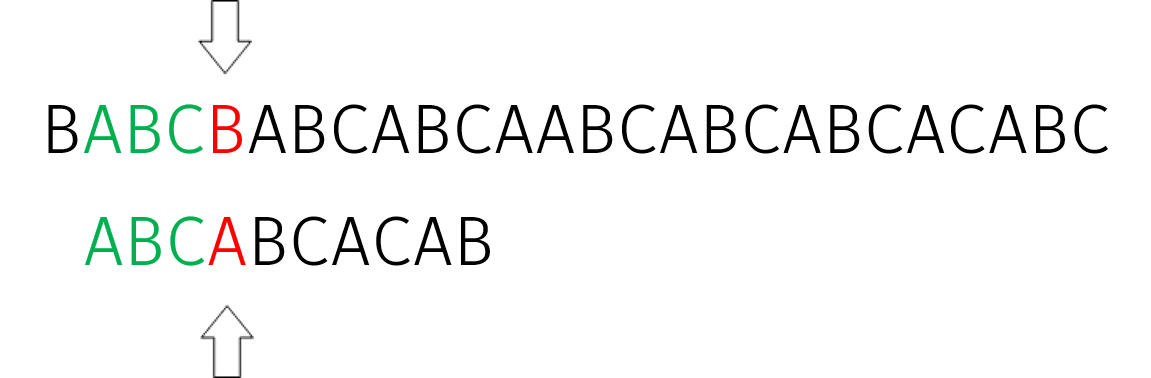
在 $j=3$ 处失配。此时我们可以得到 $S[i\dots(i+j-1)]=P[0\dots(j-1)]$。于是我们计算 $P[0\dots(j-1)]$ 的最长相等真前缀和真后缀的长度 $\pi(j-1)$。我们发现，$j$ 指针可以直接移动到 $\pi(j-1)$ 的位置并直接比较 $S[i]$ 与 $P[j]$。于是，我们令 $i=i+j$，然后循环计算 $j=\pi(j-1)$ 直到 $j \le 0 \operatorname{or} S[i]=P[j]$ 为止。

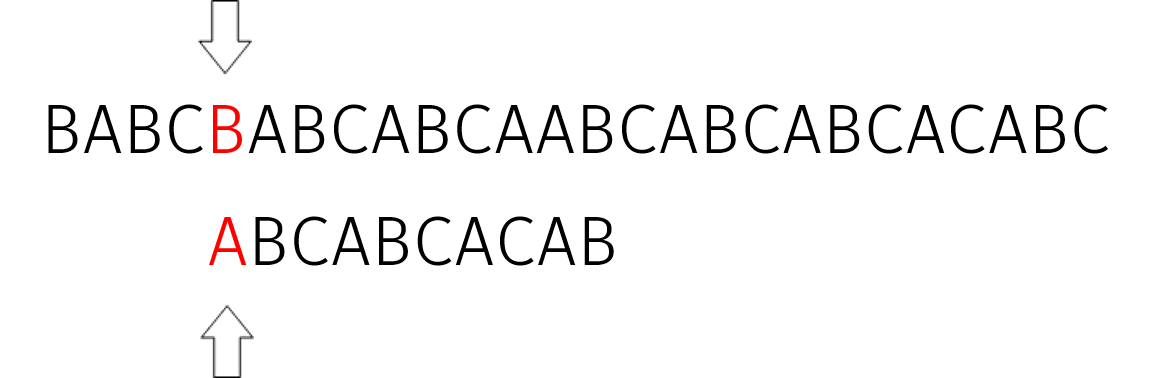
计算后可以得到：$i=4,j=0$。但由于此时 $S[i]$ 仍然不等于 $P[j]$，我们直接将 $i$ 指针右移一格继续匹配。

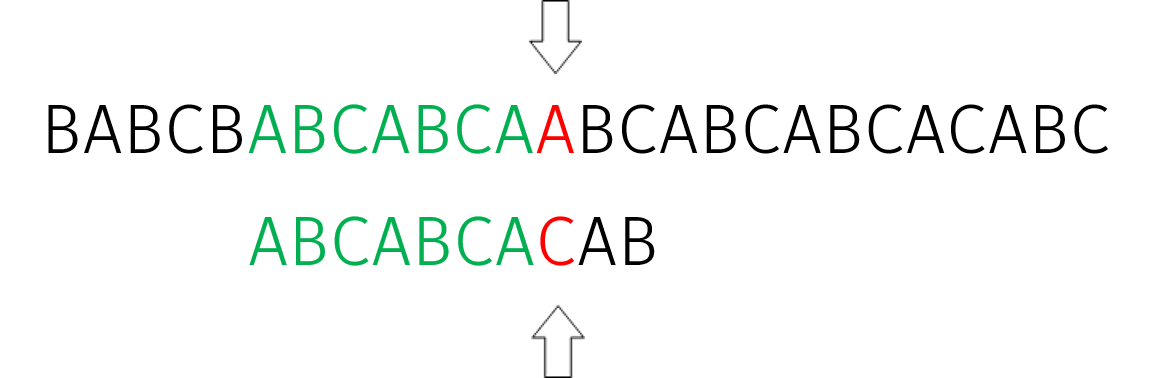
在 $j=7$ 处失配。继续重复计算 $j=\pi(j-1)$。

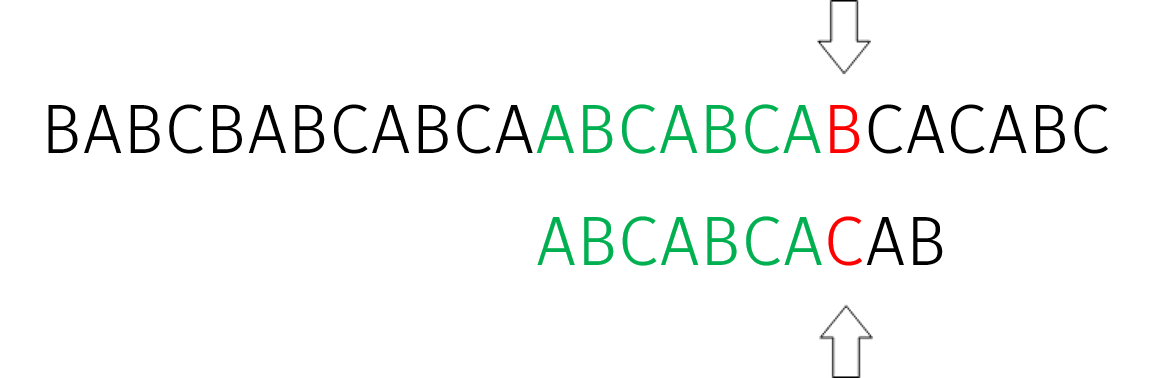
计算得到：$i=12,j=4$。继续匹配，在 $j=7$ 处失配。继续重复计算 $j=\pi(j-1)$。

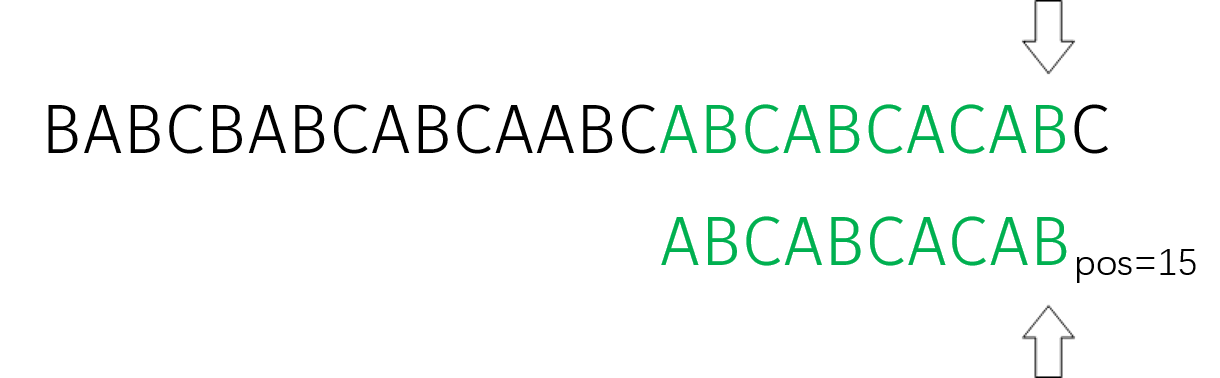
计算得到 $i=15,j=4$。此时，匹配成功，记录成功位置 $pos=15$。仿照之前的过程继续计算。

由于 $i$ 指针到达 $S$ 串末尾，停止匹配。

可以发现，$\text{KMP}$ 算法的匹配过程其实和求解前缀函数的过程十分相似。这是因为，求解前缀函数的过程其实就类似于模式串和自己匹配的过程。整个匹配过程的代码也很简单：

查看代码

int nxt[maxn];

int kmp(string s,string p) {
    int cnt = 0,n = s.size(),m = p.size();
    getNxt(p,nxt);
    for(int i = 1,j = 0;i < n;i ++) {
        while(j > 0 && s[i] != p[j]) j = nxt[j - 1];
        if(s[i] == p[j]) j ++;
        if(j == m) printf("%d\n",i - m + 1),j = nxt[j - 1],cnt ++;
    }
    return cnt;
}

利用摊还分析，我们可以得到，$\text{KMP}$ 算法的时间复杂度为 $\Theta(n+m)$。

例题 Loj #103. 子串查找

给定一个字符串 $A$ 和一个字符串 $B$，求 $B$ 在 $A$ 中的出现次数。$A$ 和 $B$ 中的字符均为英语大写字母或小写字母。$A$ 中不同位置出现的 $B$ 可重叠。

$\text{KMP}$ 模板题。直接套板子即可。

查看代码

#include <cstdio>
#include <string>
#include <iostream>

const int maxn = 1e6 + 5;
using std::string;

string a,b;
int n,m,nxt[maxn];

void getNxt(string s,int nxt[]) {
    int n = s.size();
    for(int i = 1,j = 0;i < n;i ++) {
        while(j && s[i] != s[j]) j = nxt[j - 1];
        if(s[i] == s[j]) j ++;
        nxt[i] = j;
    }
    return ;
}

int kmp(string s,string p) {
    int cnt = 0,n = s.size(),m = p.size();
    getNxt(p,nxt);
    for(int i = 0,j = 0;i < n;i ++) {
        while(j && s[i] != p[j]) j = nxt[j - 1];
        if(s[i] == p[j]) j ++;
        if(j == m) j = nxt[j - 1],cnt ++;
    }
    return cnt;
}

int main() {
    std::cin >> a >> b;
    printf("%d\n",kmp(a,b));
    return 0;
}